3. 확률 보행 프로세스
3.1 확률 보행(Random Walk)란?
- 평균과 분산이 시간이 지나도 일정하지 않은 비정상 시계열
- 시간이 지남에 따라 무작위로 이동하는 경로를 설명하는 수학적 모델
- 확률이 개입하는 다양한 현상을 설명하는 데 필수적인 모델, 자연과학, 경제학, 컴퓨터 공학 등에 응용

- yt : 현재 값
- yt-1 : 이전 시간 단계의 값
- C : 상수, 기본적으로 시계열이 가지는 평균 값
- εt : 백색 소음, 표준정규분포를 따르는 난수로 시계열에 포함된 무작위적 요소(노이즈)
이 공식에서 현재 값이 과거 값, 상수, 백색소음의 입력 값으로 결정된 함수라는 점을 기억
-> 현재 값이 과거 정보와 랜덤한 변동의 영향을 받는다는 의미!
3.1 정상성이란 ?
- 시계열의 통계적 성질이 시간에 따라 변하지 않는 상태
- 정상성 시계열*의 정의와 조건 세 가지
- 시계열의 평균이 시간에 따라 변하지 않고 일정함.
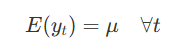
2. 시계열의 분산이 시간에 따라 일정함.

3. 시계열의 두 시점 간 공분산이 시간(t)에 의존하지 않고 시간의 차(h)에만 의존함.

- Cov() : 두 시점 사이의 선형관계를 나타냄. 크면 두 시점이 강한 상관관계, 0이면 두 시점의 관계가 없음
- 표준편차를 분모로 넣으면 상관관계가 됨.

- r(h) : 시차를 갖는 두 시점 사이의 공분산 함수
3.4 정상성 확보를 위한 데이터 변환 기법(전처리)
1. 평균 안정화
● 차분
- 차분은 시계열에서 추세, 계절성을 제거하기 위한 방법
- 특정 시점과 그 직전 시점 사이 발생하는 일련의 변화를 계산

yt : 원본 데이터
y't : 차분 후 데이터
● 이동평균 평활화(Moving Average Smoothing)
- 이동평균을 사용하면 시계열에서 단기적인 변동성을 제거하고, 전체적인 추세를 더 명확히 볼 수 있으며 평균을 안정화하는 데 도움이 됨.
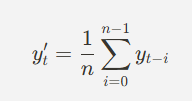
*주어진 기간의 값을 모두 더하고 평균을 내어 평균을 구하겠다는 의미.
2. 분산 안정화
● 로그 변환
- 시계열 데이터의 분산을 안정화, 큰 값을 축소시켜 분산의 변동을 줄임.
- ex) 기하급수적으로 증가하는 데이터(ex 기업 매출액, GDP), 비율 데이터

● 제곱근 변환
- 분산을 줄이는 방법으로, 양수 데이터를 대상으로 사용
- ex) 일반적인 빈도 데이터, 자연현상 데이터처럼 큰 변동성이 있는 데이터
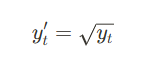
● z-score 표준화
- 데이터의 평균과 분산을 일정하게 만들기 위해 표준화를 사용
- 평균 0, 분산 1

● Box-Cox 변환
- 분산을 안정화 할 뿐만 아니라 데이터의 정규성을 보장하는 데도 유용
- 이 변환은 파라미터 람다에 따라 데이터 변환 방식을 유연하게 조정

- 람다 = 1 : 원본 데이터 유지
- 람다 = 1 : 로그 변환
- 0 < 람다 < 1 : 데이터가 클수록 변동성이 줄어들며 큰 값의 변동성을 완화
- 람다 < 0 : 데이터를 뒤집어 역변환. 큰 값은 작게, 작은 값은 크게 변환
Q : 공분산 안정화는 왜 없나요 ?
A : 평균과 분산의 안정화를 꾀하면 자연스럽게 공분산도 시간(t)에 독립적이고 시차(h)에 만 의존하는 특성을 가지기 때문!
'TIL > 머신러닝' 카테고리의 다른 글
| 시계열 데이터 분석 1 (5) | 2024.09.24 |
|---|---|
| 머신러닝| 딥러닝 (0) | 2024.08.22 |
| 비지도학습 K-Means Clustering 군집화 (0) | 2024.08.20 |
| 의사결정나무, 랜덤포레스트, KNN, 부스팅 알고리즘 (1) | 2024.08.20 |
| 데이터분석 예측 모델링 실습 (0) | 2024.08.19 |