딥러닝(Deep Learning) 이란 ?
- 머신러닝의 한 분야로, 신경세포 구조를 모방한 인공 신경망(Artificial Neural Networks) 사용

딥러닝은 머신러닝과 같은 흐름이지만, 내부 구조가 다르다. 특히, 자연어 처리와 이미지 처리에 최적화
둘 다 데이터로부터 가중치를 학습하여 패턴을 인식하고 결정을 내리는 알고리즘 개발과 관련된 AI의 분야.
(머신러닝 : 데이터 만의 통계적 관계를 찾아 예측/분류)
- 인공 신경망 : 인간의 신경세포를 모방하여 만든 Networks
- 퍼셉트론 : 인공 신경망의 가장 작은 단위
선형회귀때 예제인 키와 몸무게를 퍼셉트론으로 표현해보자.

선형 회귀에서 최소화 하려는 값은
- MSE : 에러를 제곱한 총합의 평균
- 즉, 가중치를 이리 저리 움직이면서 최소의 MSE를 도출하면 된다.
가중치를 구하는 방법
-
경사 하강법 Gradient Descent
모델의 손실 함수를 최소화하기 위해 모델의 가중치를 반복적으로 조정하는 최적화 알고리즘, 가중치를 찾기 위한 직관적이고 빠른 계산법.
만약 변수 X가 여러개 있다면 ? > 동시에 여러 개의 값을 조정하면서 최소의 값을 찾으면 된다.

최소화하려는 값을 목적 함수/소실함수 (Cost Fucntion)이라고 한다.
cost = mse, find smallest cost

기울기가 클 수록 빨리 내리간다.
step size 값을 너무 크게 할 경우 속도는 빨라지지만, 보폭이 커져 최소의 값(가중치)을 정확히 찾기 못할 수도 있음.
아래의 그림은 step size에 대한 예시

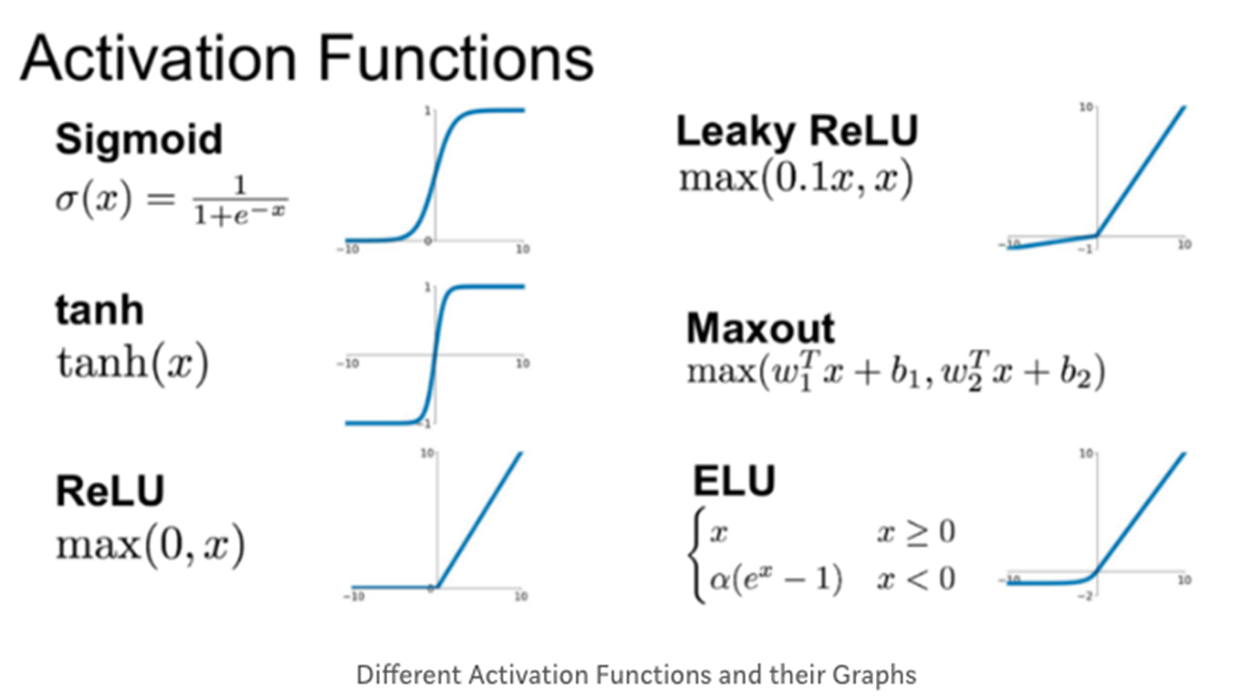
활성화 함수 Activation Functions
비선형적 분류를 위해서는 로지스틱 회귀함수 (시그모이드 함수)와 같은 활성화함수를 사용해 분류를 진행한다.

히든 레이어 Hidden Layer
비선형적 데이터로 변환했을 때의 고차원적인 특성 (이미지, 자연어)를 학습하기 위해 중간에 히든 레이어가 추가됨.
이 때, 기울기 소실 문제가 발생하는데, Relu라는 특정 활성화함수를 사용해서 해결하게 됨.

- 입력 데이터가 신경망의 각 층을 통과하면서 최종 출력까지 생성되는 과정을 순전파(Propagation)
- 신경망의 오류를 역방향으로 전파하여 각 층의 가중치를 조절하는 과정을 역전파(Backpropagation)

기울기 소실 문제 Vanishing Gradient
인공 신경망 학습 과정에서 입력 > 출력 방향의 순전파 propogation 과정과 출력 > 입력 방향의 역전파
backpropagation 과정을 진행하는데 후자의 경우(출력 방향의 순전파 propogation 과정과 출력 > 입력 방향의 역전파) 하위 레이어로 갈수록 오차의 기울기가 점점 작아져 가중치 업데이트가 안되는 현상.
각 명칭에 대한 정리
- Input Layer : 주어진 데이터가 벡터(Vector)의 형태로 입력됨.
- Hidden Layer : Input Layer와 Output Layer를 매개하는 레이어로 이를 통해 비선형 문제를 해결
- Output Layer : 최종적으로 도착하게 되는 Layer
- Activation function(활성화 함수) : 인공신경망의 비선형성을 추가하며 기울기 소실 문제를 해결
epoch란 ?
- epoch : batch* iteration, 전체 데이터가 신경망을 통과하는 한 번의 사이클 (1000 epoch = 1000번 학습)
- batch : 전체 훈련 데이터 셋을 일정한 크기의 소그룹으로 나눈 것
- iteration : batch가 학습되는 횟수, 가중치가 업데이트 되는 횟수

Epoch = batch * iteration
딥러닝 실습 Tensorflow Keras Package
tensorflow.keras.model.Sequential
- model.add: 모델에 대한 새로운 층을 추가함
- unit
- model.compile: 모델 구조를 컴파일하며 학습 과정을 설정
- optimizer : 최적화 방법, Gradient Descent 종류 선택
- loss : 학습 중 손실 함수 설정
- 회귀: mean_squared_error
- 분류: categorical_crossentropy
- metrics : 평가척도
- mse: Mean Squared Error
- acc : 정확도
- f1_score: f1 score
- model.fit: 모델을 훈련 시키는 과정
- epochs: 전체 훈련 데이터 셋에 대해 학습을 반복하는 횟수
- model.summary(): 모델의 구조를 요약하여 출력
tensorflow.keras.model.Dense: 완전 연결된 층
- unit: 층에 있는 유닛의 수. 출력에 대한 차원 개수
- input_shape:1번째 층에만 필요하면 입력데이터의 형태를 지정
- model.evaluate: 테스트 데이터를 사용하여 평가
- model.predict: 새로운 데이터에 대해서 예측 수행
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import numpy as np
from sklearn.preprocessing import StandardScaler
weights = np.array([87,81,82,92,90,61,86,66,69,69])
heights = np.array([187,174,179,192,188,160,179,168,168,174])
# sequential 모델 초기화
model=Sequential()
# 단일을 추가하기
dense_layer = Dense(units=1, input_shape=[1])
model.add(dense_layer)
model.compile(optimizer='adam',loss='mean_squared_error')
model.summary()
model.fit(weights, heights, epochs=100)
위 아키텍쳐로는 너무 간단하여 부정확할 수 있다. 따라서 히든 레이어를 생성해준다.
# hidden layer 포함한 아키텍처
model2 = Sequential()
model2.add(Dense(unit=64, activation = 'relu', input_shape=[1]))
model2.add(Dense(unit=64, activation = 'relu'))
model.add(Dense(unit=1)) #최종 숫자가 1개이기 때문에 1, 이진분류면 2, 다중분류면 그 개수만큼
model2.compile(optimizer='adam',loss='mean_squared_error')
model2.summary()
model2.fit(weights, heights, epochs=100)
여기서 더 복잡한 데이터로 복잡한 히든레이어로 모델을 만들거나, batch size 를 바꾸면서 loss를 줄일 수도 있다.
'TIL > 머신러닝' 카테고리의 다른 글
| 시계열 데이터 분석 2 (1) | 2024.09.26 |
|---|---|
| 시계열 데이터 분석 1 (5) | 2024.09.24 |
| 비지도학습 K-Means Clustering 군집화 (0) | 2024.08.20 |
| 의사결정나무, 랜덤포레스트, KNN, 부스팅 알고리즘 (1) | 2024.08.20 |
| 데이터분석 예측 모델링 실습 (0) | 2024.08.19 |